지난 글 Momentum에 이어서 이번에는 AdaGrad라는 매개변수의 Optimizer에 대해서 알아보도록 하겠습니다.
AdaGrad란?
Adaptive Gradient의 줄임말로서 지금까지 많이 변화한 매개변수는 적게 변화하도록, 반대로 적게 변화한 매개변수는 많이 변화하도록 learning late의 값을 조절하는 개념을 기존의 SGD에 적용한 것입니다.
AdaGrad의 장점
SGD에서 비등방성 함수의 경우 비효율적이라고 얘기하면서 예시를 보여드렸습니다.

지그재그로 계속 이동하게되어 실제 손실함수의 최솟값으로 이동하는데 비효율적인데 만약 학습률(learning late)을 낮춘다면 어떻게 될까요? SGD에서 손실함수의 기울기(gradient)는 벡터의 방향성을, 학습률은 벡터의 크기를 의미하는 바가 큽니다. 만약 학습률은 점진적으로 낮춘다면 지그재그로 활동하는 형태를 줄여 매개변수 y는 좀더 빠르게 손실함수의 최솟값으로 다가갈 수 있습니다.
또한 위 예시에서는 x축에 대해서는 조금씩 조금씩 이동하는데 만약 매개변수 x에 대한 학습률(learning late)를 올린다면 어떻게 될까요? 더 빠르게 최솟값에 도달 할 수 있습니다.
공식
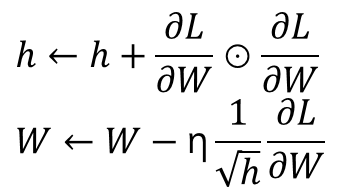
위 식에서 두 번째를 보면 h를 제외하면 기존의 SGD와 같은 갱신방법이라는 것을 알 수 있습니다. 여기에 h를 곱하여 학습률에 개입하여 위 AdaGrad의 개념을 사용할 수 있습니다. h에는 매번 갱신될때마다 해당 매개변수의 기울기값을 제곱하여 넣습니다. 즉 이런 방법을 통해서 처음에는 학습률을 높이고 많이 이동 할 수록 학습률을 낮출 수 있습니다.
결과

문제점과 해결방안
AdaGrad의 문제점은 h의 값은 항상 양으로 커지기 때문에 매개변수가 매우 크게 이동하여 h의 값이 무한대로 커진다면 해당 매개변수의 학습이 정체 될 수 있다는 점입니다. 이런점을 해결하기 위해서 RMSProp라는 새로운 방안이 있습니다.
'Machine Learning' 카테고리의 다른 글
| 머신러닝 프로젝트 개발 과정 - 0. 문제 정의 (0) | 2020.02.18 |
|---|---|
| 머신러닝 시스템의 종류( 지도, 비지도, 준지도, 강화, 배치/온라인, 사례/모델기반) (0) | 2020.02.15 |
| 신경망 학습 - (4 - 2) 모멘텀 (Momentum) (0) | 2020.01.23 |
| SGD - 비등방성 함수(anisotropy function) (0) | 2020.01.23 |
| 신경망 학습 - (4 - 1) 확률적 경사 하강법, SGD( Stochastic Gradient Descent ) (0) | 2020.01.21 |