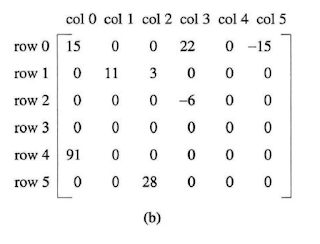
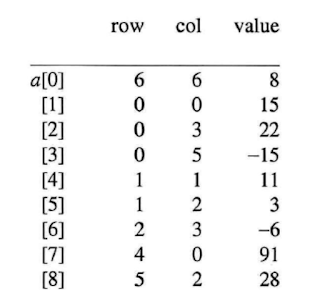
Transposing Sparse Matrix
1. 희소행렬(Sparse Matrix)이란?
희소행렬은 행렬안의 값들 중에서 0이외의 값이 희소한 행렬을 의미합니다.
따라서 대부분 0이라면 모든 값들을 표현하지 않고 0이아닌 값과 그 위치만 알고 나머지는 0이다 라고 표현을 할 수 있습니다.
평소에 그리던 행렬을
이런 방식으로 표현할 수 있습니다.(변환 방식은 생략)
2. 희소행렬의 대칭이동
위에서 봤던 간단하게 표현된 행렬을 통해서 대칭이동을 하겠습니다.
단순한 대칭이동은 그저 row와 col값을 교환해주면 간단합니다. 그러나 정렬을 유지 하고싶다면 어떻게 해야할까요?
단순 교환은 정렬이 유지되지 않습니다. 따라서 새로운 방법을 궁리해야합니다.
3. 대칭이동과 정렬
우선 기존행렬을 A, 바뀐 새로운 행렬을 B라고 합시다.
대칭이동을 하면서 정렬을 하기위해선 단순히 바꾸기보다는 적절한 위치에 A의 원소를 넣고 row,col을 바꿔주기
자 그럼 할일은 두가지 입니다.
1. row, col 바꿔주기
: 못하면 안됩니다;;
2. 적절한 위치에 넣어주기
네 이부분이 관건이 됩니다.
적절한 위치에 어떻게 넣지? 라고 생각하면 우리가 선택한 원소가 갈 장소가 적힌 배열(row_start[])을 만들어서 해결해봅시다.
그럼 자연스럽게 이 배열은 어떻게 만들지? 라고 생각 할 수 있습니다.
코딩이 아니라 머리로 넣을 장소를 생각해봅시다. 머리로 생각 할 줄 알아야 코드를 짤 수 있으니까요
그리고 이걸 보면 A에서 같은 각col 종류의 갯수들을 알면 row_start[]을 알 수 있겠네? 라는 생각을 할 수 있습니다.
구체적으로는
row_start[i]의 값은 row_start[i-1]에서 그 i-1에 해당하는 A의 col갯수를 더하면 알 수 있습니다.
그리고row_start[0]은 0번째 즉 첫번째니까 바로 1을 넣을 수 있습니다.
예를 들어 우리가 A의 열 1이 들어갈 row_start[1]을 구하고 싶다면
row_start[0]에서 A의 열중 0의 갯수를 구하고 더하면 됩니다.
예를 들어 우리가 A의 열 1이 들어갈 row_start[1]을 구하고 싶다면
row_start[0]에서 A의 열중 0의 갯수를 구하고 더하면 됩니다.
그 다음부터는 위의 규칙을 적용하면 차례로 row_start[i]를 구할수 있겠죠?
자 그렇다면 다음으로 구해야할 것들은 해당하는 A의 col갯수들이담긴 배열(col_count)입니다.
이건 A에 있는 col들을 i=1 ~ 8 까지 전체를 세어서 col_count[A[i].col]++을 하면 되겠죠?
이제 구상이 끝났으니 코드를 조져봅시다.
4. 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
#include <stdio.h>
#include <stdlib.h>
#define size 9
#define MAX_COL 6
#define MAX_ROW 6
/*
term: 행렬의 행,열 그리고 해당 값을 저장
*/
typedef struct term {
int row;
int col;
int value;
}term;
term *transposing(term A[]);
int main(void) {
term A[9] = { { 6,6,8 },{ 0,0,15 },{ 0,3,22 },{ 0,5,-15 },{ 1,1,11 },{ 1,2,3 },{ 2,3,-6 },{ 4,0,91 },{ 5,2,28 } };
term *B = transposing(A);
system("pause");
}
term *transposing(term A[]) {
//setting
//처음 부분이니 여러가지를 선언해서 세팅을 해줍시다.
// 위의 col_Count는 여기서 rowTerms로 표현했습니다.
int rowTerms[MAX_COL] = { 0 }, startPoint[MAX_COL] = { 0 };
term B[size];
B[0].col = A[0].row; B[0].row = A[0].col; B[0].value = A[0].value;
//get rowTerm
for (int i = 1; i < size; i++) {
rowTerms[A[i].col]++;
}
//get startpoint
startPoint[0] = 1;
for (int i = 1; i <MAX_COL; i++) {
startPoint[i] = startPoint[i - 1] + rowTerms[i - 1];
}
//transport to B
for (int i = 1; i < size; i++) {
int j = startPoint[A[i].col]++;
B[j].row = A[i].col;
B[j].col = A[i].row;
B[j].value = A[i].value;
}
return B;
}a
| cs |
'Computer Science > Data Structure' 카테고리의 다른 글
| Dive Data Structure with Java Collection (1) | 2022.03.10 |
|---|---|
| 2017 카카오페스티벌 예선 문제 1 - 카카오프렌즈 컬러링북 풀이 (0) | 2020.01.18 |
| 자료구조1 - Selection Sort(선택정렬) & Bineary search(이진탐색) (0) | 2020.01.18 |