신경망 학습 - 4에서는 매개변수를 갱신하는 효율적인 방법에 대해서 알아보겠습니다.
지난번에서는 학습시간을 단축시키기 위해서 미니배치를 추출하여 학습하는 SGD, 확률적 경사하강법에 대해서 알아보았습니다.
SGD는 비등방성 함수의 경우 문제점이 발생한다는 것을 알았으니 이번에는 이를 보완하기 위한 Momentum이라는 Optimizer(매개변수 갱신 방법)에 대해서 알아보도록 하겠습니다.
모멘텀이란?
모멘텀은 운동량을 의미하며 Momentum Optimizer는 매개변수의 이동에 속도를 부여하는 것을 의미합니다.
쉽게 말해서 구슬을 떨어트리면 급한 경사에서는 더 빨라지듯이 매개변수의 변화에도 속도를 부여하는 것입니다.
수식
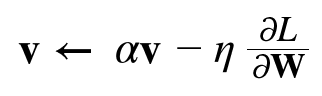
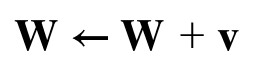
위 수식을 보면 알겠지만 매개변수를 갱신 할 때마다 기존속도에 매개변수의 기울기값을 추가하고 이 속도값을 다시 매개변수에 추가하여 매개변수를 이동시킵니다. 위에서 사용되는 알파는 만약 매개변수가 0이 되어 아무런 힘을 받지 않는다면 서서히 속도를 감소시키기 위해서 사용되며 보통 0.9를 사용합니다.
SGD와 모멘텀의 비교


모멘텀을 사용할 경우 x축은 항상 같은 방향을 가르키므로 양의 가속도로 작용하여 SGD에 비해서 지그재그의 비율이 줄어들었습니다. 그러나 y축은 번갈아 상충하여 속도가 안정적이지 못합니다.
모멘텀의 장점
모멘텀은 위처럼 SGD에 비해서 효율적인 학습을 할 수 있다는 점 뿐만 아니라 SGD가 가지고 있는 또 다른 문제인 Local Minima를 해결 할 수 있습니다.
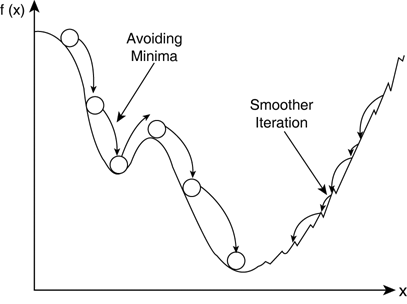
SGD의 경우 Local Minima에 빠져서 더 이상 학습을 진행할 수 없는 문제가 있습니다. 모멘텀을 사용한다면 속도의 개념때문에 깊이가 낮은 Local Minima는 위 그림처럼 뛰어넘어 계속 진행 할 수 있습니다.
'Machine Learning' 카테고리의 다른 글
| 머신러닝 시스템의 종류( 지도, 비지도, 준지도, 강화, 배치/온라인, 사례/모델기반) (0) | 2020.02.15 |
|---|---|
| 신경망 학습 - (4 - 3) AdaGrad(Adaptive Gradient) (0) | 2020.01.28 |
| SGD - 비등방성 함수(anisotropy function) (0) | 2020.01.23 |
| 신경망 학습 - (4 - 1) 확률적 경사 하강법, SGD( Stochastic Gradient Descent ) (0) | 2020.01.21 |
| 신경망 학습 - (3) 오차 역전파(Backpropagation) (0) | 2020.01.20 |