들어가며
이전 글에서는 샘플과 결괏값 사이의 관계를 1차식으로 구하는 선형 회귀에 대해서 알아보았습니다. 선형회귀만으로는 2차 이상의 관계를 구할 수 없으므로 이번에는 다항관계를 구하는 다항회귀에 대해서 알아보도록 하겠습니다.
목차
- 정의
- 코드 구현
- 다항회귀의 특징
1.1정의
앞서 말했듯 다항회귀는 2차 이상의 방정식을 통한 관계 구현입니다. 이를 구하기 위해서는 기존 특성의 거듭제곱을 구하고 이를 새로운 특성으로서 샘플에 추가한 후 선형회귀(LinearRegression)를 구하는 것입니다.
이렇게 한 경우 x^2과 x^1을 서로 다른 특성으로 인식하여 선형회귀는 두 개의 특성에 맞는 결과를 구하기 위해 정규방정시을 사용합니다. 코드구현을 통해서 쉽게 알아보도록 하겠습니다.
1.2 코드구현
1. 2차방정식 형태의 데이터 생성
import numpy as np
import numpy.random as rand
np.random.seed(42)
m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 0.5 * X**2 + X + 2 + np.random.randn(m, 1)
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([-3, 3, 0, 10])
save_fig("quadratic_data_plot")
plt.show()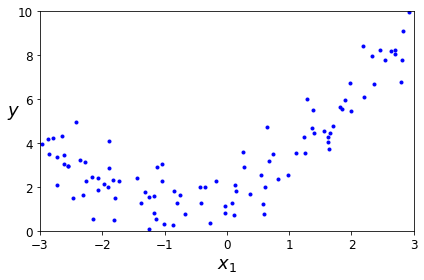
2. PolynomialFeatures모듈을 사용하여 거듭제곱 형태의 특성 추가
from sklearn.preprocessing import PolynomialFeatures
poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)
X[0]
#result = array([-0.75275929])
X_poly[0]
#result = array([-0.75275929, 0.56664654])3. LinearRegression모듈을 통해서 선형관계 분석
lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)
lin_reg.intercept_, lin_reg.coef_
#resutl = (array([1.78134581]), array([[0.93366893, 0.56456263]]))4. 최종 결과
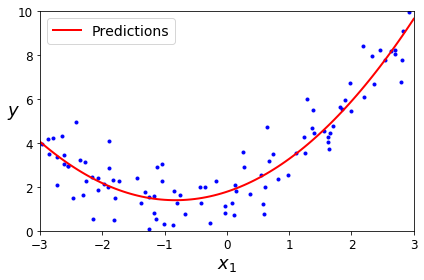
1.3 다항회귀의 특징
PolynomialFeatures 모듈에 데이터를 입력할 때 두 개 이상의 데이터를 입력할 경우(x, y, z ... ) 이 모듈은 각 데이터만의 거듭제곱이 아니라 서로 다른 데이터들의 교차항(xy, x^2 y, xy^2 ... )을 추가하므로 특성 사이의 관계를 파악하는데 용이합니다.
하지만 입력 데이터의 수와 거듭제곱(degree)의 수가 증가할 수록 교차항이 기하급수적으로 증가하여 학습 시간 또한 기하급수적으로 증가하므로 이를 유의해야합니다.
'Machine Learning' 카테고리의 다른 글
| 머신러닝 모델 - 3.정규화(regularization, 과대적합 완화 ) (0) | 2020.04.17 |
|---|---|
| 머신러닝 모델 - 학습곡선(다항 회귀의 차원 설정) (0) | 2020.04.16 |
| 머신러닝 모델 - 1. 선형회귀(Linear Regression) (0) | 2020.04.15 |
| 머신러닝 프로젝트 - 10. 최상의 모델과 오차 분석 (1) | 2020.03.10 |
| 머신러닝 프로젝트 - 9. 모델 세부 튜닝(그리드 탐색, 랜덤 탐색) (0) | 2020.03.10 |