들어가며
이번 글에서는 문제를 해결하는 가장 단순한 방법인 완전탐색 또는 Brute-Force알고리즘에 대해서 알아보도록 하겠습니다.
목차
- 정의
- 사용개념(재귀호출)
- 재귀 호출을 완전탐색에 사용하는 방법
- 문제 예시 : Boggle Game
- 시간복잡도 분석
정의
Brute-Force는 직역하면 무식하게 풀기라는 의미입니다. 문제가 주어졌을 때 일어날 수 있는 모든 경우의 수를 계산해서 원하는 출력값을 얻는 것을 의미합니다. 모든 경우의 수를 탐색하므로 완전탐색(Exhaustive Solving)이라고도 불립니다. 이는 컴퓨팅 자원을 극심하게 소모하기 때문에 입력값이 작을 것으로 기대될때만 사용하는 것이 좋습니다.
간단하게 예를 들어보겠습니다. 열 명의 학생을 한 줄로 세우려고 하는데 서로 사이가 안 좋은 학생들을 붙여서 세우면 안된다는 조건이 있습니다. 이 조건을 만족하면서 열 명을 세우는 경우의 수를 구하는 문제는 어떻게 풀어야 할까요? 가장 단순한 방법은 열명의 학생을 한 줄로 세우는 모든 경우의 수를 만들고 사이가 안 좋은 학생들이 떨어져 있는 경우의 수를 세면됩니다. 10!은 대략 360만 가지의 경우의수를 가지지만 이는 컴퓨터가 1초안에 처리할 수 있기 때문에 완전탐색을 사용하는것이 적합한 문제입니다.
사용개념(재귀호출)
자 이제 정의를 알아보았으니 코드로 어떻게 구현해야 할 지 고민할 차례입니다. 여기에서 우리는 재귀호출이라는 개념을 사용할 수 있습니다.
우선 재귀호출의 정의부터 차근차근 설명하겠습니다.
재귀호출은 "자기 자신을 호출하는 함수"입니다.
.

자신을 호출하면 함수 하나가 할 일을 반복해서 호출할 수 있습니다. 반복문이랑 비슷하다고 생각하면됩니다.
하지만 조건없이 계속 호출한다면 위 처럼 무한으로 반복되기에 중간에 멈추기 위한 종료조건(Base Case)이 필요합니다.

재귀 호출을 완전탐색에 사용하는 방법
다시 위 예에서 10명을 한줄로 세우는 경우의수로 돌아가봅시다.
10명을 한 줄로 세우는 경우의 수를 출력하는 문제를 푸는 과정은 다음과 같습니다.
1. 10명 중 한 명을 선택해서 줄에 추가
2. 9명 중 한 명을 선택해서 줄에 추가
3. 8명 중 한 명을 선택해서 줄에 추가
.
.
10. 1명 중 한 명을 선택해서 줄에 추가
비슷한 점이 보이시나요? 10번의 과정은 선택하는 인원의 차이만 있지 방법은 모두 똑같습니다.
이 처럼 경우의 수를 구하는 문제는 비슷한 부분문제들로 쪼갤 수 있습니다.
그렇다면 비슷한 부분문제를 코드로 작성하는 방법은 무엇이 있을까요?
바로 재귀함수입니다!
결국 경우의 수는 부분문제로 쪼갤 수 있고 이를 코드로 작성하는데는 재귀함수가 적합하므로 완전탐색 알고리즘은 재귀함수로 작성합니다.
예제 문제 : Boggle Game
완전 탐색의 정의와 문제 풀이방법을 알아보았으니 실제로 문제를 풀어보도록 하겠습니다.
문제: Boggle Game
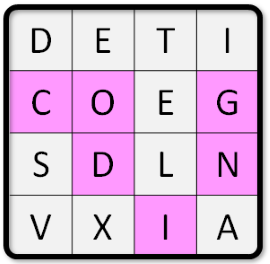
설명 : N x N의 필드에 각 칸마다 하나의 문자가 새겨져 있고 상하좌우, 대각선 방향으로 이어서 하나의 단어를 찾을 수 있는지 찾는 문제입니다. (위의 경우 coding을 찾아야합니다. )
완전탐색으로 해결하기
문제를 해결하기 위한 과정을 만들어봅시다.
1. 하나의 칸을 선택하고 단어의 첫 번째 글자가 있는지 확인
2. 상하좌우,대각선 방향 등 총 8가지의 방향에 두 번째 글자가 있는지 확인
3. 두 번째 글자에서 다시 상하좌우,대각선 방향 등 8가지 방향에 세 번째 글자가 있는지 확인
.
.
.
위 과정을 보니 계속해서 글자가 일치하는지 확인하고 8가지 방향을 탐색하는 과정을 반복합니다.
이렇게 반복하는 과정을 정의했으니 재귀함수로 이 정의를 구현하고 문제를 해결해봅시다.
const int dx[8] = { -1, -1, -1, 1, 1, 1, 0, 0};
const int dy[8] = { -1, 0, 1, -1, 0, 1, -1, 1};
/*
함수 정의 : 보드의 위치를 받아 글자가 일치하는지 확인하고 다음 8방향 탐색
*/
bool hasWord(int x, int y, int pos) {
//종료조건1: 넘겨받은 보드의 위치가 범위를 초과한 경우
if (x < 0 || x >= 5 || y < 0 || y >= 5)
return false;
//종료조건2: 글자가 일치하지 않는 경우
if (Board[x][y] != Word[pos])
return false;
//종료조건3: 글자수와 탐색 횟수가 일치하는 경우 = 모든 단어의 글자가 일치하는 경우
if (Word.size() == pos + 1)
return true;
bool ret = false;
for (int d = 0; d < 8; ++d) {
//8방향의 결과값들을 하나씩 확인 후 하나라도 true를 반환하면 true반환
//모든 방향의 결과값들이 false일 경우 false를 반환
if (hasWord(x + dx[d], y + dy[d], pos + 1)) {
ret = true;
break;
}
}
return ret;
}시간복잡도 분석
보글게임을 문제를 해결했으니 이제 위 알고리즘이 얼마나 시간이 걸리는지 계산하기 위해서 시간복잡도를 계산해보겠습니다.
시간복잡도는 항상 최악의 경우를 생각해서 작성해야합니다. 예를 들어 찾고자하는 단어가 aaaab이고 보드에는 전부 a만 있다고 가정합시다. 이런 경우 위 알고리즘은 모든경우를 탐색하기에 8^4의 경우의 수를 탐색합니다. 즉 단어의 길이가 n 일때 8^(n-1)개의 경우의 수를 탐색하기에 하나의 단어를 찾는데 O(8^n)의 시간복잡도가 기대됩니다. 이는 기하급수적으로 경우의 수가 상승하므로 단어의 길이가 길고 보드의 크기가 클 경우 다른 알고리즘을 사용하는 것이 좋습니다.
'Computer Science > Algorithm' 카테고리의 다른 글
| [코딩테스트] 2020 KAKAO BLIND RECRUITMENT문자열 압축 풀이 (0) | 2021.09.07 |
|---|